"kelaskita.com"
where g is the vector representing the local gravitational acceleration. This g can be determined by observing how a nearby freely-falling object accelerates relative to your chosen reference frame. See section 2 for more about the definition of “gravity”. See reference 1 for a discussion of how to define “mass”.
Equation 1 says nothing about what may be causing the local gravitational field; the only thing that matters is the absolute acceleration of your chosen reference frame. Of course it is often convenient to attach your reference frame to some nearby planet, in which case the planet makes a large contribution to g via the law of universal gravitation (equation 4) ... but that is rarely (if ever) the only contribution to g, for reasons discussed in section 2.
Remarks:
1. A pencil in an orbiting space ship is weightless according to an observer in the ship’s reference frame.
2. A pencil in orbit is not weightless according to an observer in a ground-based reference frame. Let’s be clear: it is the frame that matters. The pencil does not become weightless because of the motion of the pencil, but because of the motion of the reference frame.
Mass is 100% independent of the choice of frame.
Weight is 100% dependent on the choice of frame.
3. Notation: Many books adopt the convention that the vector W (boldface) has magnitude W (non-boldface) where W := |W|. Similarly the vector g has magnitude g := |g|. This works OK for books and for web pages, where boldface is easy to achieve, but when you’re writing things by hand it is not very convenient. For this reason (among others), I recommend the following convention: Vectors should be written without any decoration, i.e. without arrows over them, without lines under them, or anything like that. Boldface is optional, never required. So we are free to use non-bold W to represent a vector. If/when it is convenient to use boldface, bold W means the same thing as non-bold W. If we ever need the scalar magnitude of W, we write |W|. (It is not worth the trouble to come up with a more compact notation for |W|.) This convention works fine for all media, including handwritten notes, books, email, and so forth. This convention is consistent with (and practically required by) more advanced work involving multivectors. See reference 2 for more on this.
4. The W and g vectors are directed downward. I don’t think this is part of the definition of W or g; instead, I think it is the definition of “downward”.
5. Since g is a vector, it is improper to ask whether it is positive or negative. There is no “>” relationship defined for vectors (except possibly in one-dimensional vector spaces, which we exclude from consideration, since we are interested in multi-dimensional motion). Therefore you can’t ask whether a vector is “>0” or “<0”. Of course |g|, the magnitude of g, is non-negative, but that doesn’t tell us anything we didn’t already know (since the magnitude of any vector is automatically non-negative).
Therefore, when folks ask about the sign of g, you know they are asking an unanswerable question. It is often difficult to figure out what prompted the question.
Sometimes they intended to ask about some particular component of g in some chosen reference frame. The answer could be positive or negative, depending on what reference frame they choose. If the +Z direction points downward, then gz is positive, whereas if the +Z direction points upward, then gz is negative. This is a common source of confusion, because different folks are free to choose different reference frames.
Sometimes they intended to ask about projection of g along the direction of some other physically-significant vector in the problem. Again this depends on which other vector they’re talking about, but at least the answer to this question is physically-meaningful and observer-independent, once the question has been spelled out in sufficient detail.
Also: when people seem to be confused about the “sign” of g, often the main problem lies elsewhere. It may have to do with velocity versus speed, as discussed in reference 3.
6. Some people prefer to speak of the force due to gravity (or the force “of” gravity) instead of weight. Similarly they prefer to denote it Fg instead of W. (Usually Fg means exactly the same thing as W.) This allows us to write nice expressions such as:
Fg := gravitational force
ag := local gravitational acceleration
Fg = m ag
(2)
without even mentioning weight, as opposed to
W := weight, i.e. gravitational force
g := local gravitational acceleration
W = m g
(3)
Equation 2 has the advantage of logic and elegance, but it hasn’t caught on very widely.
7. Most people live placidly near the surface of the earth, where to a fair approximation |g| is constant, which means there is a one-to-one correspondence between weight and mass. This explains why non-experts commonly blur the distinction between weight and mass.
However, the distinction remains important, and will never die out. For example, as previously mentioned, it is very convenient to say that astronauts see themselves as weightless but not massless.
Also, for careful work, you need to take into account the fact that |g| depends on where you are on the earth’s surface. The variation is on the order of one percent. See reference 4.
8. The weight of an object in the lab frame will be very slightly time-dependent for various reasons including weather-related changes in the mass of air overhead, solar gravity, lunar gravity, et cetera.
9. I find it unhelpful to define or recognize any distinction between “true weight” and “apparent weight”. Weight is weight. Let’s just call it the weight. If the weight relative to one accelerated reference frame is different from the weight relative to another, so be it. The situation is symmetrical; there is no basis for deciding which weight is “true” and which is “apparent”. Even if you could decide that one frame is “true” and the other only “apparent”, what are you going to do when there are three mutually-accelerated frames?
10. Depending on context, there are various things that the word “gravity” could mean, and what the symbol “g” could mean. Some more-explicit, less-ambiguous terminology is discussed in section 2.
11. The weight will not in general equal the total downward force. Weight includes only the force due to the local gravitational field, not the forces due to buoyancy, air currents, magnetic fields, bungee cords, or anything else. However, in a fair number of practical situations we can arrange that these non-gravitational contributions are negligible, in which case the weight can be well approximated by measuring the total downward force, perhaps by letting the object rest on a spring-scale. (Of course the scale should be at rest in the chosen reference frame.)
It is important to use a spring scale, not just any old scale, because there are plenty of scales on the market that measure mass instead of weight, or measure some weird combination of mass and weight. (Scale manufacturers can get away with considerable vagueness, since they assume their scales will be operated on the Earth’s surface, where |g| is reasonably uniform and well-known. See section 3.3.)
12. Similarly, there some grade-school textbooks that try to define weight (not just approximate it) by saying weight is “whatever the scale reads”. Such a definition cannot be taken seriously, for a number of reasons. The problems include:
This is an “instrumental” definition. Like all instrumental definitions, it is open to all sorts of questions about what happens if the instrument is miscalibrated, or outright broken. There are serious philosophical questions here, and also nontrivial practical questions when we start asking about your weight on the moon, or your weight aboard a space station, since scales that behaved fine on the earth might well misbehave in other situations.
You might try to solve this class of problems by talking about an “ideal” scale, but defining what you mean by that is no easier than defining “weight” from scratch.
If you were to take the scale reading literally, you would be in error, because you would have neglected the buoyancy correction.
Almost all scales are intended to measure mass, not weight. For example, consider kitchen scales. If the cookie recipe calls for 1/4 pound of butter, the intention is presumably to use the same mass of butter even if I am baking cookies on the moon.
In practice it is not particularly uncommon to find two scales in the same room, one of which (to a good approximation) responds to mass while the other (to a good approximation) responds to weight.
Perhaps the most serious objection is that this notion of weight applies only to objects that are stationary or at least unaccelerated relative to the scale. For objects that are free to move, indeed even partially free to move (such as an Atwood machine, as shown in figure 1, or even a simple pendulum), the true weight is still there, as evidenced by the acceleration of the object, but the actual force exerted on the scale will not be equal to the weight mg.
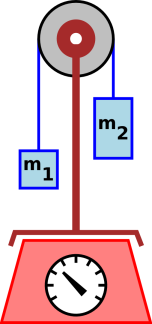
Figure 1: Atwood Machine on a Scale
A student on a scale, hopping up and down, will illustrate the same point, namely a scale-reading that is wildly time-dependent and therefore different from what we would like to call “the” mass or “the” weight.
Another notorious example is an hourglass on a scale. The flow of the sand causes the center of mass of the hourglass to move downward. In some rare cases, the motion of the center of mass will be uniform (to a sufficient approximation) in which case it doesn’t affect the reading. In other cases, depending on the shape of the sand-chambers and other factors, the motion of the center of mass will be nonuniform. This counts as an acceleration of the hourglass as a whole, in which case the situation is analogous to figure 1, and the force on the scale will not be equal to the weight mg.
Bottom line: Defining weight in terms of whatever “the” scale reads runs a large (and quite unnecessary) risk of spreading misconceptions.
Equation 1 says nothing about what may be causing the local gravitational field; the only thing that matters is the absolute acceleration of your chosen reference frame. Of course it is often convenient to attach your reference frame to some nearby planet, in which case the planet makes a large contribution to g via the law of universal gravitation (equation 4) ... but that is rarely (if ever) the only contribution to g, for reasons discussed in section 2.
Remarks:
1. A pencil in an orbiting space ship is weightless according to an observer in the ship’s reference frame.
2. A pencil in orbit is not weightless according to an observer in a ground-based reference frame. Let’s be clear: it is the frame that matters. The pencil does not become weightless because of the motion of the pencil, but because of the motion of the reference frame.
Mass is 100% independent of the choice of frame.
Weight is 100% dependent on the choice of frame.
3. Notation: Many books adopt the convention that the vector W (boldface) has magnitude W (non-boldface) where W := |W|. Similarly the vector g has magnitude g := |g|. This works OK for books and for web pages, where boldface is easy to achieve, but when you’re writing things by hand it is not very convenient. For this reason (among others), I recommend the following convention: Vectors should be written without any decoration, i.e. without arrows over them, without lines under them, or anything like that. Boldface is optional, never required. So we are free to use non-bold W to represent a vector. If/when it is convenient to use boldface, bold W means the same thing as non-bold W. If we ever need the scalar magnitude of W, we write |W|. (It is not worth the trouble to come up with a more compact notation for |W|.) This convention works fine for all media, including handwritten notes, books, email, and so forth. This convention is consistent with (and practically required by) more advanced work involving multivectors. See reference 2 for more on this.
4. The W and g vectors are directed downward. I don’t think this is part of the definition of W or g; instead, I think it is the definition of “downward”.
5. Since g is a vector, it is improper to ask whether it is positive or negative. There is no “>” relationship defined for vectors (except possibly in one-dimensional vector spaces, which we exclude from consideration, since we are interested in multi-dimensional motion). Therefore you can’t ask whether a vector is “>0” or “<0”. Of course |g|, the magnitude of g, is non-negative, but that doesn’t tell us anything we didn’t already know (since the magnitude of any vector is automatically non-negative).
Therefore, when folks ask about the sign of g, you know they are asking an unanswerable question. It is often difficult to figure out what prompted the question.
Sometimes they intended to ask about some particular component of g in some chosen reference frame. The answer could be positive or negative, depending on what reference frame they choose. If the +Z direction points downward, then gz is positive, whereas if the +Z direction points upward, then gz is negative. This is a common source of confusion, because different folks are free to choose different reference frames.
Sometimes they intended to ask about projection of g along the direction of some other physically-significant vector in the problem. Again this depends on which other vector they’re talking about, but at least the answer to this question is physically-meaningful and observer-independent, once the question has been spelled out in sufficient detail.
Also: when people seem to be confused about the “sign” of g, often the main problem lies elsewhere. It may have to do with velocity versus speed, as discussed in reference 3.
6. Some people prefer to speak of the force due to gravity (or the force “of” gravity) instead of weight. Similarly they prefer to denote it Fg instead of W. (Usually Fg means exactly the same thing as W.) This allows us to write nice expressions such as:
Fg := gravitational force
ag := local gravitational acceleration
Fg = m ag
(2)
without even mentioning weight, as opposed to
W := weight, i.e. gravitational force
g := local gravitational acceleration
W = m g
(3)
Equation 2 has the advantage of logic and elegance, but it hasn’t caught on very widely.
7. Most people live placidly near the surface of the earth, where to a fair approximation |g| is constant, which means there is a one-to-one correspondence between weight and mass. This explains why non-experts commonly blur the distinction between weight and mass.
However, the distinction remains important, and will never die out. For example, as previously mentioned, it is very convenient to say that astronauts see themselves as weightless but not massless.
Also, for careful work, you need to take into account the fact that |g| depends on where you are on the earth’s surface. The variation is on the order of one percent. See reference 4.
8. The weight of an object in the lab frame will be very slightly time-dependent for various reasons including weather-related changes in the mass of air overhead, solar gravity, lunar gravity, et cetera.
9. I find it unhelpful to define or recognize any distinction between “true weight” and “apparent weight”. Weight is weight. Let’s just call it the weight. If the weight relative to one accelerated reference frame is different from the weight relative to another, so be it. The situation is symmetrical; there is no basis for deciding which weight is “true” and which is “apparent”. Even if you could decide that one frame is “true” and the other only “apparent”, what are you going to do when there are three mutually-accelerated frames?
10. Depending on context, there are various things that the word “gravity” could mean, and what the symbol “g” could mean. Some more-explicit, less-ambiguous terminology is discussed in section 2.
11. The weight will not in general equal the total downward force. Weight includes only the force due to the local gravitational field, not the forces due to buoyancy, air currents, magnetic fields, bungee cords, or anything else. However, in a fair number of practical situations we can arrange that these non-gravitational contributions are negligible, in which case the weight can be well approximated by measuring the total downward force, perhaps by letting the object rest on a spring-scale. (Of course the scale should be at rest in the chosen reference frame.)
It is important to use a spring scale, not just any old scale, because there are plenty of scales on the market that measure mass instead of weight, or measure some weird combination of mass and weight. (Scale manufacturers can get away with considerable vagueness, since they assume their scales will be operated on the Earth’s surface, where |g| is reasonably uniform and well-known. See section 3.3.)
12. Similarly, there some grade-school textbooks that try to define weight (not just approximate it) by saying weight is “whatever the scale reads”. Such a definition cannot be taken seriously, for a number of reasons. The problems include:
This is an “instrumental” definition. Like all instrumental definitions, it is open to all sorts of questions about what happens if the instrument is miscalibrated, or outright broken. There are serious philosophical questions here, and also nontrivial practical questions when we start asking about your weight on the moon, or your weight aboard a space station, since scales that behaved fine on the earth might well misbehave in other situations.
You might try to solve this class of problems by talking about an “ideal” scale, but defining what you mean by that is no easier than defining “weight” from scratch.
If you were to take the scale reading literally, you would be in error, because you would have neglected the buoyancy correction.
Almost all scales are intended to measure mass, not weight. For example, consider kitchen scales. If the cookie recipe calls for 1/4 pound of butter, the intention is presumably to use the same mass of butter even if I am baking cookies on the moon.
In practice it is not particularly uncommon to find two scales in the same room, one of which (to a good approximation) responds to mass while the other (to a good approximation) responds to weight.
Perhaps the most serious objection is that this notion of weight applies only to objects that are stationary or at least unaccelerated relative to the scale. For objects that are free to move, indeed even partially free to move (such as an Atwood machine, as shown in figure 1, or even a simple pendulum), the true weight is still there, as evidenced by the acceleration of the object, but the actual force exerted on the scale will not be equal to the weight mg.

Figure 1: Atwood Machine on a Scale
A student on a scale, hopping up and down, will illustrate the same point, namely a scale-reading that is wildly time-dependent and therefore different from what we would like to call “the” mass or “the” weight.
Another notorious example is an hourglass on a scale. The flow of the sand causes the center of mass of the hourglass to move downward. In some rare cases, the motion of the center of mass will be uniform (to a sufficient approximation) in which case it doesn’t affect the reading. In other cases, depending on the shape of the sand-chambers and other factors, the motion of the center of mass will be nonuniform. This counts as an acceleration of the hourglass as a whole, in which case the situation is analogous to figure 1, and the force on the scale will not be equal to the weight mg.
Bottom line: Defining weight in terms of whatever “the” scale reads runs a large (and quite unnecessary) risk of spreading misconceptions.
"Life Is a Learning"

No comments:
Post a Comment